Introduction

La macroségrégation désigne les variations chimiques à grande échelle qui apparaissent lors de la solidification, sous l’effet de déplacements inégaux et de l’accumulation localisée d’éléments d’alliage. À l’échelle locale, la microségrégation se développe à l’intérieur des dendrites ou entre cellules primaires. En revanche, la macroségrégation affecte des volumes entiers du lingot, provoquant des hétérogénéités significatives qui compromettent leurs performances métallurgiques et mécaniques. Cela représente un défi industriel important où des variations locales en carbone ou en éléments d’alliage critiques peuvent réduire la qualité finale1,2. Ce phénomène est particulièrement accentué lors de la coulée en lingot, car les grandes dimensions et les gradients thermiques complexes favorisent les mouvements de convection et la redistribution du soluté3.

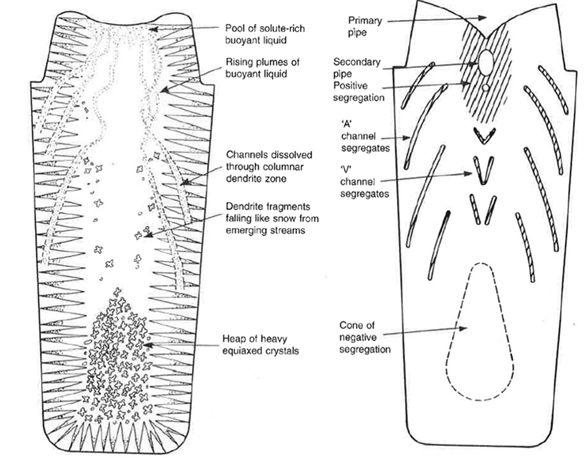
La Figure 1 ci-dessous, illustre les principaux mécanismes physiques mis en jeu lors de la solidification d’un lingot. La différence de densité entre le liquide enrichi et appauvri en soluté génère des mouvements ascendants qui forment des canaux dans la zone dendritique colonnaire. Des fragments de dendrites se détachent, sédimentent et s’accumulent en cristaux équiaxes plus denses au fond du lingot. Ces transferts induisent une répartition hétérogène du soluté avec des zones de ségrégation positive (pipes et canaux) et une zone centrale de ségrégation négative4,5.

 

(a)                                                                   (b)

Figure 1: Schéma illustrant les mécanismes de formation de la macroségrégation lors de la solidification d’un lingot4. (a) Circulation de liquide enrichi en soluté, dissolution de canaux dans la zone dendritique colonnaire et formation de cristaux équiaxes. (b) Répartition typique des zones deségrégation positive (pipes primaires et secondaires, canaux « A » et « V ») et de la zone de ségrégation négative (cône central).

 

Pour anticiper et limiter ces phénomènes de ségrégation, la modélisation de la solidification des lingots s’appuie sur des modèles éléments finis qui visent à reproduire les principaux mécanismes physiques couplés. Parmi ceux-ci figurent notamment la convection thermosolutale induite par les gradients de température et de concentrations des solutés3,6–10, le retrait de solidification3,10, la sédimentation des grains équiaxes9,11 et la déformation de la zone pâteuse3.

Cependant, la modélisation complète et prédictive de l’intégralité de ces phénomènes couplés, constitue un défi majeur, en particulier pour des configurations industrielles complexes. Le logiciel  THERCAST® , issu de la recherche du Centre de Mise en Forme des Matériaux (CEMEF-MINES Paris PSL), vise à relever ce défi en intégrant progressivement ces effets dans un cadre de simulation cohérent et évolutif.

Dans une étude précédente, le modèle de macroségrégation thermosolutale enrichi d’un calcul analytique de la capacité calorifique Cp, a été validé sur un système binaire bien documenté (Hebditch et Hunt12). Cette validation a permis d’établir une base de référence fiable pour le développement de modèles plus complexes et représentatifs des conditions industrielles. Dans cette continuité, le présent article propose d’enrichir le précédent modèle, par une extension du calcul analytique de Cp à des alliages multi-binaires.

Enrichissement du calcul de la capacité calorifique dans lecas d’un alliage multi-composant

Le modèle de macroségrégation induite par la convection thermosolutale repose sur plusieurs hypothèses simplificatrices : la solidification est supposée purement colonnaire, sans formation de grains équiaxes et le solide est considéré comme fixe et indéformable, sans prise en compte du retrait de solidification. Ce modèle couple les équations de conservation de la masse, de la quantité de mouvement, de l’énergie et de la concentration solutale, afin de prédire l’évolution des champs de vitesse, de température et de composition pendant la solidification. Dans ce travail, ces équations ont été adaptées pour permettre l’application du modèle à un alliage multi-binaire, notamment par la prise en compte de la dépendance de la capacité calorifique à la composition chimique.

La mécanique des fluides est décrite par l’équation de Navier–Stokes moyennée sur la phase liquide dans un volume élémentaire représentatif10 :


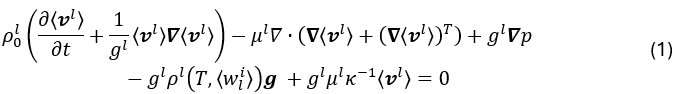
où ρ0lest la densité du liquide correspondant à la température de référence Tref, ⟨v l⟩ est le champ de vitesse moyen du liquide, gl est la fraction liquide, p est le champ de pression, g représente le vecteur gravité, ⟨wli⟩ représente la concentration moyenne en soluté i dans la phase liquide, et κ la perméabilité de type Carman-Konzeny, exprimée en fonction de l’espacement secondaire des bras dendritiques λ2:

La densité du liquide ρ0lest supposée constante, sauf dans le terme de gravité où l’approximation de Boussinesq est utilisée. Cette approximation prend désormais en compte la contribution de chacune des espèces chimiques de l’alliage multi-composant :

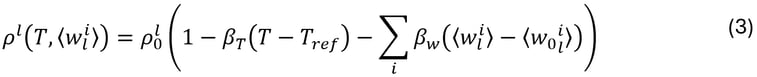
où βT et βw sont respectivement les coefficients de dilatation thermique et solutale, tandis que ⟨w0li⟩ et ⟨wli⟩ représentent respectivement la concentration nominale et moyenne du soluté i dans la phase liquide.

Le liquide est supposé comme incompressible, l’équation de conservation de la masse se simplifie comme :

Letransfert thermique pendant la solidification est modélisé par l’équation de conservation de l’énergie :

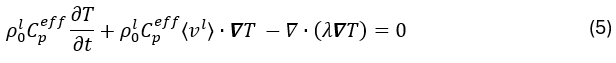
où λ est la conductivité thermique et Cpeff est la capacité calorifique effective qui inclut la contribution de la chaleur latente L selon Ahmad et al.13

Dans un système multi-composant, le calcul de Cpeff se complexifie car les équilibres thermodynamiques à l’interface solide/liquide dépendent de plusieur séléments d’alliage, chacun influençant différemment les températures de liquidus et de solidus. La relation gs(T) qui évalue la fraction solide en fonction de la température selon le modèle de microségrégation Brody-Flemings14 avec une approximation linéaire des diagrammes de phase, ne peut plus être explicitée directement car la température dépend non seulement de gs mais aussi des concentrations locales de chaque soluté. Pour cela, l’équilibre est résolu numériquement pour chaque fraction solide donnée, ce qui donne la relation implicite T(gs) suivante :

7

 

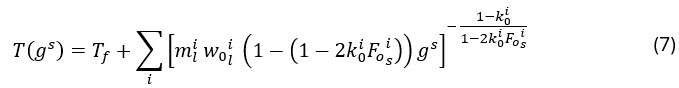
où mli représente la pente de la ligne liquidus pour l’élément i de l’alliage, k0i est le coefficient de de partition de l’élément i,FOsi est le nombre de Fourier qui mesure ladiffusivité du soluté i dans le solide et Tfreprésente la température de fusion de l’élément pur. Cette relation estconditionnée par la température de solidus Tsol selon laformulation de Vannier15 qui bloque le front desolidification. Le problème est ainsi inversement reformulé en calculant ladérivée partielle de T(gs) par rapport à gs.Par conséquent, Cpeff est alors déterminée commesuit :

6-1

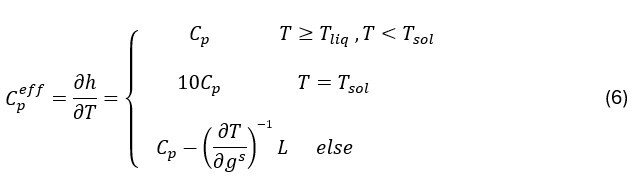
Tliq étant la température de liquidus. Cette approche permet de mieux tenir compte des effets de la chaleur latente et d’améliorer la prédiction des fractions liquide et solide.

Enfin, le transport solutal pour chaque soluté i est gouverné par l’équation suivante :

8

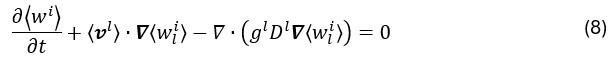
dans laquelle la diffusion des espèces chimiques est considérée négligeable devant le transport convectif et ne concerne que la phase liquide. La méthode de séparation des variables de Voller-Prakash10 est ensuite utilisée pour calculer d’abord l’inconnu ⟨wi⟩, puis en déduire ⟨wli⟩.

Validation dumodèle sur le cas d’un alliage multi-binaire

Afin de valider l’enrichissement du calcul de la capacité calorifique, nous nous sommes appuyés sur les travaux de thèse de Liu7, appliqués à un alliage multi-composant. Cette démarche permet de confronter nos résultats à ceux obtenus avec deuxc odes de référence bien établis dans la littérature : le code SOLID16 basé sur une approche volumes finis, et le code R2SOL17, développé pour la simulation bidimensionnelle par éléments finis.

Le cas test de Liu modélise la solidification de l’alliage multi-binaire Fe – 0,2 wt% C dans une cavité carrée de 100 mm de côté, illustrée en Figure 2. Les parois de la cavité sont supposées adiabatiques, à l’exception des faces latérales soumises à un flux thermique de type Fourier. Une vitesse de liquide nulle est imposée sur l’ensemble des parois.

 

9-1Figure 2: Schéma de la géométrie et des conditions aux limites appliquées pour la simulation de la solidification d’un alliage multi-binaire, dans le cadre du cas test proposé par Liu.

 

Une stratégie de « non-couplage »est adoptée dans les simulations réalisées à l’aide de SOLID et R2SOL, dans lesquelles le système est considéré comme localement fermé, sans enrichissementdu bain liquide et les termes diffusifs sont négligés. Cette stratégie de non-couplage consiste à résoudre à chaque pas de temps, de manière séquentielle et sans itération forte, les équations de conservation de l’énergie, du soluté et de la quantité de mouvement. Dans notre cas, la simulation a été réalisée avec couplage en utilisant le modèle THERCAST® enrichi par le calcul analytique de la capacité calorifique et sa dépendance de la composition chimique.

Les résultats de la ségrégationrelative de la concentration massique de carbone : 12, sont illustrés en Figure 3, en comparaison avec les résultats de la littérature. La distribution de carbone prévue par THERCAST® est en bon accord avec les résultats de de SOLID et R2SOL.En effet, une ségrégation positive est observée en partie supérieure, et négative en partie inférieure, conséquence de la remontée du liquide enrichi en carbone dans la zone pâteuse. De plus, le résultat de THERCAST® révèle des structures de ségrégation plus fines (Figure 3(c)) en comparaison avec les résultats de référence. Par ailleurs, l’adoption d’une stratégie de couplage itératif, telle que proposée par Bellet et al.18, améliore davantage la précision, notamment en termes de concentrations minimale et maximale en carbone, au prix d’un surcoût computationnel.

 

10Figure 3: Cartographies de concentration massique en carbone simulées selon la règle de levier après 10 min de solidification de l’alliage multi-binaire Fe – 0,2 % C, à l’aide de (a) SOLID® et (b)R2SOL®, en comparaison avec (c) le résultat du modèle enrichi de THERCAST® pour des maillages grossier (gauche) et fin (droite).

 

Afin d’ajuster le niveau de fidélité thermodynamique en fonction des ressources de calcul disponibles et de la précision attendue, une démarche repose sur la réactivation de types d’enrichissement (0 et 1) au-delà du schéma simplifié de type 2, afin de mieux représenter l’enrichissement local du bain liquide. Dans ce cadre, le chemin de solidification est imposé localement pour chaque volume élémentaire représentatif (REV) selon l’une de ces approches :

  • Enrichissement de type 2 : le chemin de solidification est fixé par la concentration nominale initiale, en supposant un état initial totalement liquide. Ni l’enrichissement du liquide, ni celui de la zone pâteuse ne sont pris en compte. Ce schéma correspond à la stratégie de non-couplage de R2SOL, où le chemin de solidification est prédéfini et reste inchangé pendant toute la simulation ;
  • Enrichissement de type 1 : le chemin est défini à partir de la dernière concentration du liquide avant le début de la solidification de chaque REV. Seul l’enrichissement du bain liquide est pris en compte, le chemin étant figé dès le démarrage de la solidification locale ;
  • Enrichissement de type 0 : le chemin de solidification est mis à jour en continu à partir de la concentration locale instantanée. L’enrichissement du liquide et de la zone pâteuse est ainsi pris en compte, et le chemin évolue dynamiquement au fil de la solidification.

La Figure 4 ci-dessous présente la distribution de la ségrégation en manganèse à l’état solide, calculée pour trois configurations distinctes. Avec un enrichissement classique de type 2 et une capacité calorifique considérée constante, la Figure 4(a) montre une cartographie limitée de la macroségrégation. L’adoption d’un calcul analytique de Cpeff, tout en conservant l’enrichissement de type 2, met en évidence davantage de détails, avec des zones de ségrégation positive et négative plus marquées (Figure 4(b)). Enfin, l’utilisation combinée d’un enrichissement de type 0 et du calcul analytique de Cpeff permet d’obtenir une répartition légèrement plus affinée de la ségrégation du manganèse dans certaines zones du lingot (Figure 4(c)).

 

11

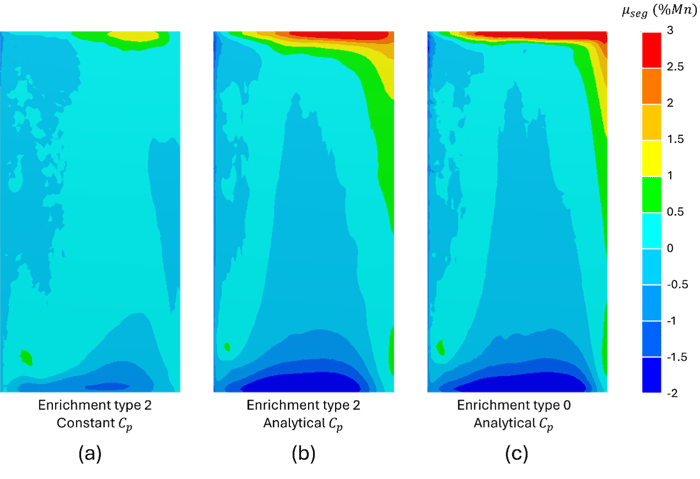
Figure 4: Cartographies de la ségrégation relative en manganèse après 1000 s de solidification, simulées pour trois configurations : (a) enrichissement de type 2 avec Cp constant, (b) enrichissement de type 2 avec Cp calculée analytiquement, et (c) enrichissement de type 0 avec Cp calculée analytiquement.

 

Conclusion

Cet article montre la capacité du modèle THERCAST® à prédire avec précision la macroségrégation dans les alliages multicomposants, tout en offrant à l’utilisateur la possibilité d’adapter le niveau de détail en fonction des contraintes de temps de calcul.

L’amélioration du calcul de la capacité calorifique et l’extension des options d’enrichissement du chemin de solidification renforcent la cohérence thermodynamique et la fiabilité des prédictions. Ces avancées assurent une continuité de comportement entre les cas de référence binaires et les cas multi-binaires plus représentatifs des conditions réelles. Avec ces développements, THERCAST® met à disposition des industriels un outil de simulation robuste, précis et flexible pour mieux maîtriser la qualité des produits solidifiés.

Ne manquez pas nos prochaines publications, qui dévoileront des améliorations encore plus poussées du modèle, incluant notamment la prise en compte de la sédimentation des grains équiaxes.

 


References
1.    Yan, G., Han, L., Li, C., Luo, X. & Gu, J. Effect of macrosegregation on the microstructure and mechanical properties of a pressure-vessel steel. Metallurgical and Materials Transactions A 48, 3470–3481 (2017).
2.    Pickering, E. & Bhadeshia, H. Macrosegregation and microstructural evolution in a pressure-vessel steel. Metallurgical and Materials Transactions A 45, 2983–2997 (2014).
3.    Rivaux, B. Simulation 3D éléments finis des macroségrégations en peau induites par déformations thermomécaniques lors de la solidification d’alliages métalliques. (2011).
4.    Campbell, J. Castings. (Elsevier, 2003).
5.    Ludwig, A., Wu, M. & Kharicha, A. On macrosegregation. Metallurgical and Materials Transactions A 46, 4854–4867 (2015).
6.    Gouttebroze, S. Modélisation 3D par éléments finis de la macroségrégation lors de la solidification d’alliages binaires. (2005).
7.    Liu, W. Modélisation par éléments finis des phénomènes thermomécaniques et de macroségrégation dans les procédés de solidification. Thèse de doctorat, Ecole Nationale Supérieure des Mines de Paris (2005).
8.    Carozzani, T. Développement d’un modèle 3D Automate Cellulaire-Éléments Finis (CAFE) parallèle pour la prédiction de structures de grains lors de la solidification d’alliages métalliques. (2012).
9.    Nguyen, T.-T.-M. Multiscale finite element modeling of macrosegregation and grain transport. Thèse de doctorat, Ecole Nationale Supérieure des Mines de Paris (2015).
10. Saad, A. Modélisation par level set des macroségrégations induites par le retrait à la solidification. (2016).
11. Ettroudi, H. Modélisation numérique multi-échelle des structures de solidification, de la macroségrégation et de la Transition Colonnaire-Equiaxe. Thèse de doctorat, Ecole Nationale Supérieure des Mines de Paris (2021).
12. Hebditch, D. J. & Hunt, J. D. Observations of ingot macrosegregation on model systems. Metallurgical transactions 5, 1557–1564 (1974).
13. Ahmad, N. et al. Numerical simulation of macrosegregation: a comparison between finite volume method and finite element method predictions and a confrontation with experiments. Metallurgical and Materials Transactions A 29, 617–630 (1998).
14. Rappaz, M. & Dantzig, J. A. Solidification. (EPFL Press, 2009).
15. Vannier, I., Combeau, H. & Lesoult, G. Numerical model for prediction of the final segregation pattern of bearing steel ingots. Materials Science and Engineering: A 173, 317–321 (1993).
16. Vannier, I. Modélisation de la solidification des lingots d’acier. Thèse de doctorat, Institut National Polytechnique de Lorraine (1995).
17. Gaston, L. Résolution numérique par éléments finis d’un modèle de solidification pour alliages métalliques multiconstitués. CEMEF internal  report (1999).
18. Bellet, M., Fachinotti, V., Gouttebroze, S., Liu, W. & Combeau, H. A 3D-fem model solving thermomechanics and macrosegregation in binary alloys solidification. Symposium on Solidification Processes and Microstructures, in Honor of Wilfried Kurz, TMS Annual Meeting 41–46 (2004).