Microstructure forms the critical bridge between process parameters, material behaviour, and final properties of parts. Numerical modelling of microstructure evolutions is a fundamental means for predicting final material behaviour. This approach significantly reduces the time and cost associated with developing and optimizing new materials.
For metal forming modelling to be accurately predictive, it must incorporate microstructure concepts, such as grain size and dislocation density evolutions, or solid phase transformations, which is essential to meet the increasingly strict demands on material properties in industrial applications. The ultimate objective implies a correct description of the major physical mechanisms1 occurring in metals during thermomechanical processing, notably continuous (CDRX), discontinuous (DDRX) and post- (PDRX) dynamic recrystallization, solid/solid phase transformations (SSPT), grain growth (GG) or Ostwald ripening (OR), etc.
Thanks to DIGIMU®, a software based on a FE-LS (Finite Element – Level-Set) framework, full field simulations of industrial processes and heat treatments with GG, DDRX, PDRX or SRX, with or without second phase particles (SPP)2–7 are rendered possible.
In what follows, we discuss the recent developments in DIGIMU® that delve deeper into physics at the mesoscopic scale, leading to more advanced features in its models in terms of thermomechanical conditions and material types. These developments were carried out in close collaboration with our academic partner, the Centre for Material Forming (CEMEF, MINES ParisTech), as part of the ToRealIMotion Chair and supported by the ANR – FRANCE (French National Research Agency).

Simulate coupled SPP and grain evolutions

The Smith-Zener pinning, or the phenomenon where grain boundaries (GB) are pinned by SPP in the microstructure, is widely used to control grain size during the forming of alloys or superalloys. Predictive tools are crucial for modelling accurately this phenomenon and thereby optimizing the final grain size. In the previous version of DIGIMU®, SPP were described as holes in the microstructure without considering hypotheses on their size, morphology, interface energies with grains, or their dragging force. This conventional method is effective as long as the evolution of SPP during the simulation is not sought8,9. However, SPP are subject to several diffusive mechanisms, such as precipitation/dissolution, Ostwald ripening, etc., causing them to evolve throughout the process. In order to address this evolution, a first method implemented in DIGIMU®, relies on the LS formalism to describe the particles boundaries similarly as the GB description10,11. The implementation of this method allows simulating the evolution of two distinct particle populations, coupled with GG, strain induced boundary migration, DRX, PDRX and SRX. User-friendliness, compatibility, CPU time and accuracy have been optimized. Particle evolution laws are described in a userroutine module, so that they can be adapted or modified to fit at most the material’s behaviour.

The potential of this module is demonstrated by simulating the microstructural evolution of a γ−γ′ nickel-based superalloy under a simple heat treatment11, and a good agreement of the simulation with experimental results is proved regarding γ’ dissolution (check this article by De Micheli et al. to learn more).

A more advance microstructural evolution was then simulated, and the result is shown in the animation below. When the actual γ′ fraction is smaller than the γ′ equilibrium fraction, particle nucleation occurs proportionally to this gap. At the beginning of the heat treatment, under the solvus temperature, the material is out of equilibrium and has no precipitates. Rapidly, precipitates start growing until the equilibrium fraction of 5% is reached. Then Ostwald ripening begins where the particle fraction remains constant from 350 s to 1250 s, but the particles number decreases as smaller ones dissolve, and bigger ones grow. Beyond 1250 s, the temperature is increased progressively over the solvus. The equilibrium particles fraction decreases to reach 0, followed by the effective particles fraction and number. Finally, all particles are dissolved, GB are progressively released from particles pinning, and a fast grain growth occurs.

 

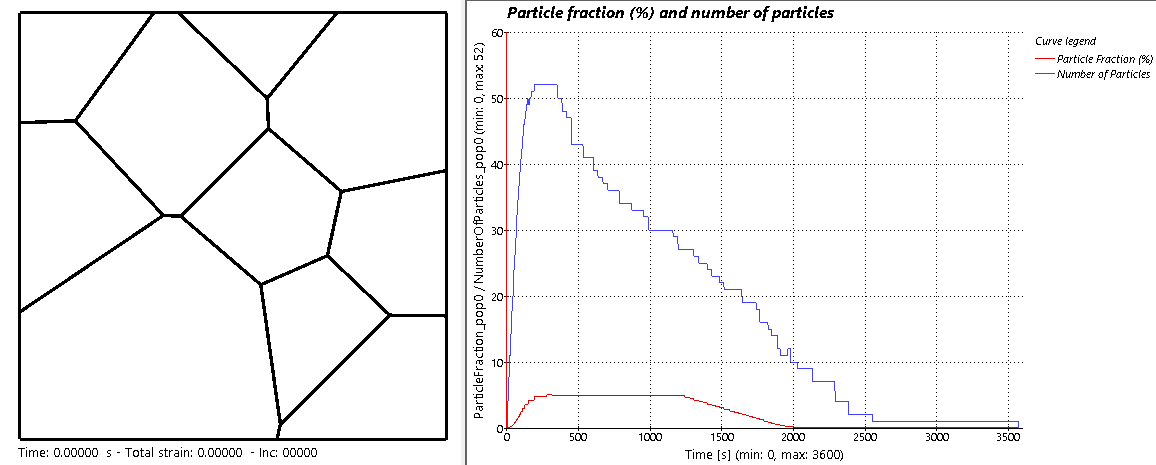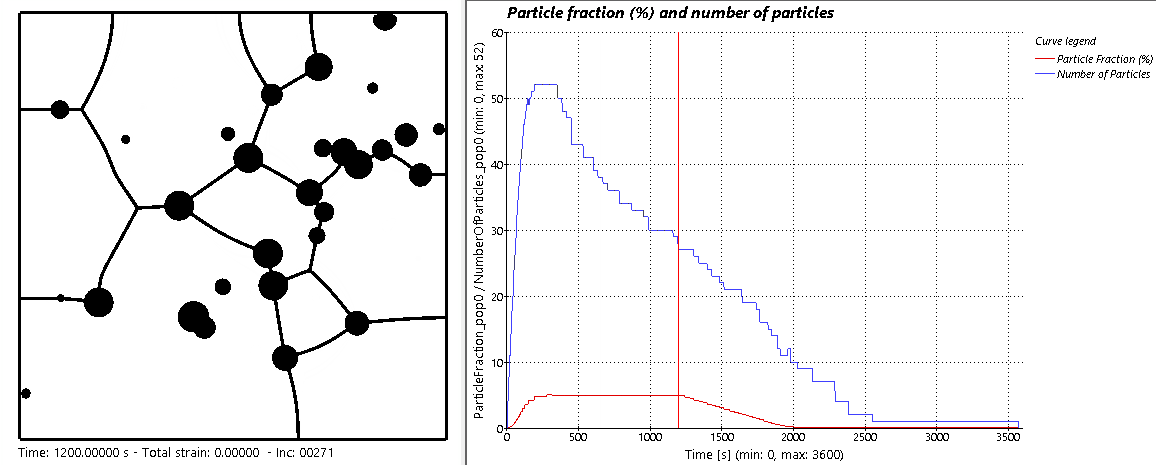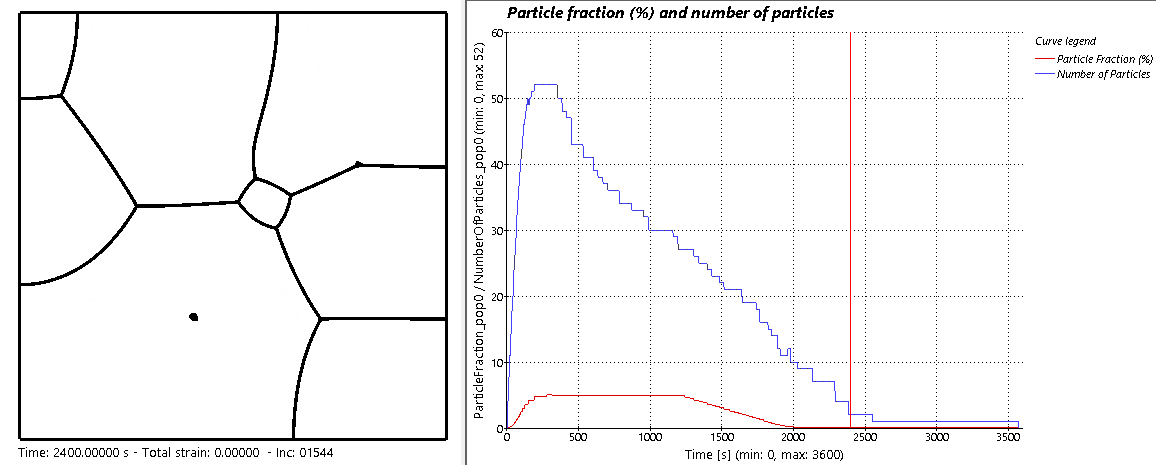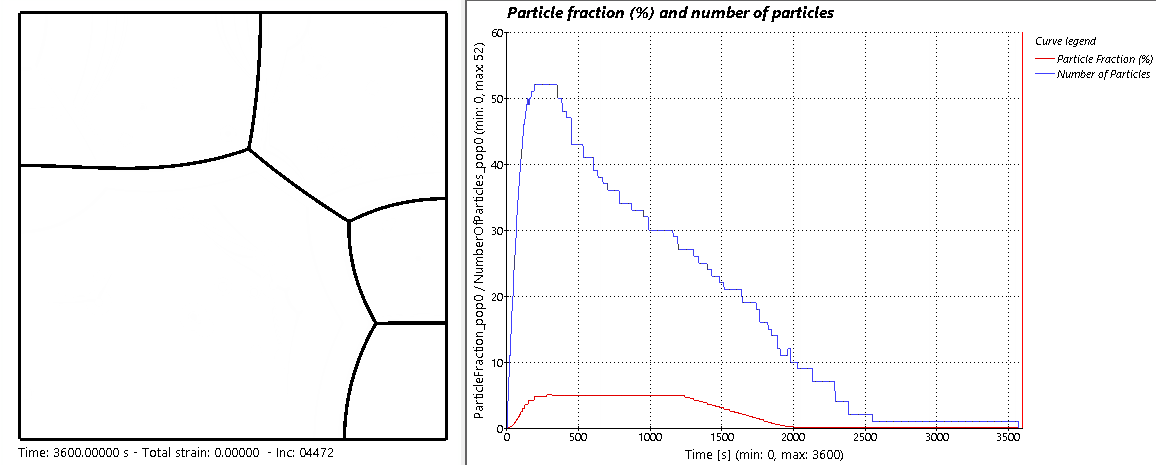
Nickel base alloy.gif

Microstructural evolution of a γ−γ′ nickel-based superalloy, illustrated along a graph showing the evolution of the particle fraction and number as a function of time.

Simulate CDRX with an evolutive population of SPP 

The LS-FE approach was largely considered in the DDRX context for low stacking-fault energy materials. In the case of high-stacking fault energy materials, the consideration of progressive formation and evolution of subgrains becomes essential. Dislocations could rearrange to form new low-angle grain boundaries (LAGB) or accumulate into preexisting LAGB. In the CDRX context, grain formation is induced by the progressive reorganization of dislocations into subgrains with a progressive increase in the misorientation angle between these subgrains12. Grand et al. propose an LS-FE framework to address this mechanism, by incorporating the Gourdet-Montheillet model13–15. This framework retains the global density evolution law defined for DDRX, while taking into account the following mechanisms of evolution of dislocations: rearrangement into LAGB that bound new subgrains, stacking into preexisting LAGB and absorption during high-angle grain boundary (HAGB) migration.

Based on this approach, a second method was implemented in DIGIMU® introducing a full-field CDRX module. This method has been applied to zircaloy-4 (Zy-4). Recrystallization of initially equiaxed grains of Zy-4 during hot extrusion has been experimentally studied, identified, and simulated at Framatome Components Research Centre13–15. A simulation of the polycrystal under hot deformation at a strain of 1 and a velocity of 1 s−1 is depicted below. A direct comparison of the simulated evolution of dislocation densities with experimental observations shows a promising agreement.

Image3Simulated and experimental Zy-4 microstructures with dislocation density distribution after 1 s of hot deformation at 1 s−1 and a hold for 25 s and 100 s at 650 °C.

To go further, we coupled these features together. In fact, Zy-4 can present some precipitates under certain conditions, with a solvus temperature close to that of the heat treatment. Therefore, we simulated the microstructural evolution by considering the effect of the precipitates during the PDRX phase of 200 s as shown in the animation below. The boundary migration is shown to be slightly modified by the presence of precipitates, with some kind of pinning. However, the latter is still not enough to really block the boundaries and the recrystallization. Additional simulations show that with a denser population of precipitates, the effect of pinning is more pronounced. In a second variant, we increase the size of the precipitates instead of their number. Because of their bigger size, we noticed that they need more time to dissolve, without being completely dissolved at the end of the 200 s PDRX. CDRX.gif

Simulated microstructure during CDRX, coupled with precipitation evolution.

 

Conclusions and Perspectives 

Simulations at the polycrystal level are now recognized as powerful tools for understanding and predicting microstructure evolution in industrial manufacturing. In this context, DIGIMU® 5.0 continues to evolve through our dedicated development efforts, recently incorporating two major advancements. These enhancements expand its capability to model a broader range of materials and thermal pathways. Two new methods have been integrated in userroutine modules and can be adapted or modified to fit the material. Future versions of DIGIMU® will introduce even more advanced functionalities to refine microstructure modelling across a wider range of materials. These enhancements aim to provide unparalleled precision and expand the software’s capabilities for tackling diverse industrial challenges.

Discover DIGIMU®'s new features and elevate your microstructure simulations today!

 

References

  1. Humphreys, J., Rohrer, G. S. & Rollett, A. Recrystallization textures. Recrystallization and related annealing phenomena 431–468 (2017).
  2. Agnoli, A. et al. Development of a level set methodology to simulate grain growth in the presence of real secondary phase particles and stored energy–Application to a nickel-base superalloy. Computational Materials Science 89, 233–241 (2014).
  3. Brüggemann, H. et al. Korngrößenvorhersage beim Freiformschmieden von Inconel 718 mit DIGIMU®. massivUMFORMUNG 2021, 50–54 (2021).
  4. De Micheli, P. et al. DIGIMU®: Full field recrystallization simulations for optimization of multi-pass processes. in vol. 2113 (AIP Publishing, 2019).
  5. Maire, L. et al. Modeling of dynamic and post-dynamic recrystallization by coupling a full field approach to phenomenological laws. Materials & Design 133, 498–519 (2017).
  6. Scholtes, B. et al. 3D level set modeling of static recrystallization considering stored energy fields. Computational Materials Science 122, 57–71 (2016).
  7. Villaret, F. et al. Probabilistic and deterministic full field approaches to simulate recrystallization in ODS steels. Computational Materials Science 179, 109646 (2020).
  8. Agnoli, A. et al. Selective growth of low stored energy grains during δ sub-solvus annealing in the Inconel 718 nickel-based superalloy. Metallurgical and Materials Transactions A 46, 4405–4421 (2015).
  9. Scholtes, B. et al. Full field modeling of the Zener pinning phenomenon in a level set framework-discussion of classical limiting mean grain size equation. in 497–503 (2016).
  10. Alvarado, K., Florez, S., Flipon, B., Bozzolo, N. & Bernacki, M. A level set approach to simulate grain growth with an evolving population of second phase particles. Modelling and Simulation in Materials Science and Engineering 29, 035009 (2021).
  11. Alvarado, K. et al. Dissolution of the primary γ′ precipitates and grain growth during solution treatment of three nickel base superalloys. Metals 11, 1921 (2021).
  12. Humphreys, J., Rohrer, G. S. & Rollett, A. Recrystallization textures. Recrystallization and related annealing phenomena 431–468 (2017).
  13. Gaillac, A., Grand, V., Arsen, A., Gaillard, Q. & Bernacki, M. Towards multi-scale modeling of zirconium alloys recrystallization and application to thermo-mechanical processes optimization. Key Engineering Materials 926, 443–451 (2022).
  14. Grand, V. Characterization and modeling of zircaloy-4 recrystallization during hot forming. (Université Paris sciences et lettre, 2022).
  15. Grand, V., Flipon, B., Gaillac, A. & Bernacki, M. Simulation of continuous dynamic recrystallization using a level-set method. Materials 15, 8547 (2022).

Download the flyer